This article will talk about something as simple as one equation: the Tsiolkovski equation, also known as “the rocket equation”. Simple as it may be, this equation laid down the foundations of rocketry and space propulsion. It still dictates major design choices in all forms of space travel.
The man that first derived this equation, Konstantin Tsiolkovski (1857-1935), is considered one of the founding fathers of astronautics. Even the most modern space systems are designed considering this equation. Understanding it is key to understanding how space travel is the way it is today.
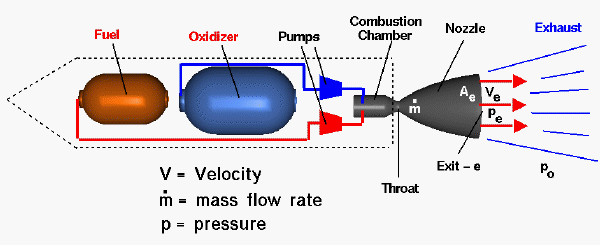
As said in the previous article “Understanding Space Propulsion”, the only possible mechanism for the production of thrust is ejecting mass in high speeds. How big can this thrust be? Calculating it is simple. We only need to apply the law of conservation of linear momentum. Let me remind you that linear momentum is the mass of a system times its speed, an expression of the inertia of the system. If there is no external force on a system, the linear momentum of that system will not change. Interestingly enough, the definition of “force” itself arises from this idea: the mechanism by which a system changes the linear momentum of another system is a force.
Let’s consider the following system: the rocket and the fuel contained within it at a given time. This is a basic principle of engineering and physics: isolating something and studying how it interacts with the rest of the Universe. In this case, let’s suppose that there is no force (no gravity, no pressure) exerted on the system. Over a period of time we will call Δt , the rocket will eject a quantity of mass Δm at a speed Δv (relative to the rocket).
Source: www.aerospaceweb.org
Since there is no force exerted on the whole system, it’s momentum will not change, so if mass is ejected in one direction, the rocket will accelerate in the other direction, increasing its speed in a value ΔV , as in the following equation:
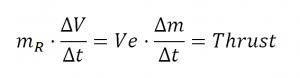
The rocket will feel this interaction with the ejected mass as thrust, a force propelling it to one direction. This equation is only valid for very small a mounts of ejected mass, because it doesn’t take into account the change in rocket mass caused by the propulsion. However, it gives good insight on what makes a spacecraft move: ejecting as much mass as possible, with the highest possible speed (notice that the relevant magnitude is the speed relative to the rocket). The lighter the rocket, the bigger the acceleration.
Considering a propulsion manoeuver with a constant ejection speed (which is a typical case), this equation can be integrated, obtaining the renowned Tsiolkovski rocket equation, which is valid for longer maneuvers:
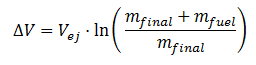
This simple formula simply changed the world: it describes the relationship between al major parameters in space travel: thruster characteristics and necessary propellant for a given velocity increase. This equation sets the basic guidelines for space mission design. It stresses the importance of weight saving in space missions. For a given mission, a total acceleration of the spacecraft must be achieved (this is known as the DeltaV budget). For example, going to the Moon requires a DeltaV of about 16 km/s, applied in different phases of flight. Ejection speed is normally limited to about 4km/s for technological reasons.
This means that taking 1kg of payload to the Moon would require about 54 kg of fuel. That explains why mass saving is so vital in space missions: each extra kilo of mass requires extra fuel to be accelerated, and this extra fuel would require even more extra fuel to be carried with the spacecraft…
For that reason, rockets are built in stages: once the fuel of one stage is burned out, the structure containing it (such as tanks and pumps) can be jettisoned, thus lowering the mass to be accelerated by the rest of the fuel in the next stages.
For the same reason, a lot of effort has been put into developing propulsion technologies with higher ejection speeds: these allow less fuel consumption and higher usable payloads. The Tsiolkovski equation has far-reaching consequences that cannot be treated only in one article. This topic will be addressed in detail on the next article of the “Space Propulsion” series, here, at Techforspace.