After laying down the foundations of modern rocketry with the Tsiolkovsky equation in the last chapter of the “Space Propulsion” series, it is now time to use it as a way to know how to optimize the design of a given thruster system. Evidently, there are countless factors to be taken into account in the design of a thruster, many of which depend on the mission profile. Heavy launchers such as the Ariane 5 require a very different kind of propulsion than the attitude control systems of observation satellites. This chapter intends to talk about one of the most fundamental design criteria in space propulsion along with mass saving: specific impulse. Understanding specific impulse is key to understand priorities in thruster design.
Specific impulse is a parameter that allows the comparison of the efficiency of thrusters of different size and type. It is commonly known as “Isp”, and is defined as the ratio between the provided thrust and the propellant mass flow rate (how many kilograms per second this thruster ejects) times the gravity acceleration at Earth sea level:
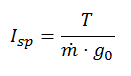
T= provided thrust , m= propellant mass flow rate, g0= gravity acceleration at sea level
It may seem weird that the acceleration of gravity is used for this definition. It makes no difference, since it is the same for all rockets – but this, changes the units of Isp to seconds. In other words, this makes the comparison from american, russian or european rockets much easier.
Isp has a clear physical meaning: if the Isp of one thruster is 50% than the Isp of another one, it means that it can generate 50% more thrust with the same flow of propellant. Considering that propellant mass is usually severely limited or, at least, very expensive, one can begin to grasp the importance of maximizing Isp. Another way to see it is taking the Tsiolkovsky equation. For a thruster in space, thrust is given by:
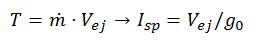
Specific impulse is actually proportional to the ejection speed. In short, the main physical quantity so as to increase Isp is the ejection speed of the thruster (this notion is complicated when considering an atmospheric flight).
Now, let’s imagine a satellite being put into orbit. For a given orbit, the acceleration needed is known, and therefore, the initial mass of the manoeuvre (limited by launcher capacity). According to the Tsiolkovsky equation, the final mass put into orbit will be:
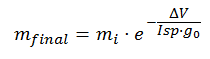
What this equation tells is that not only does the final mass delivered into orbit increase with Isp, but that it has an exponential effect. A 10% increase in Isp can easily generate a 20% increase in final mass.
Saturn V before launch: part of the success of the Apollo mission was due to the high Isp cryogenic thrusters. Source: NASA
This can make an enormous difference in a space mission: it can allow greater payloads, greater ranges, or it can even be the decisive factor that makes a mission possible. For that reason, an astounding amount of effort has always been put into developing new thruster technologies with higher specific impulses.
In the next chapters of the “Space Propulsion” series we will go deeper on that with “A tailor-made thruster” and “Thruster technologies”.

